 |
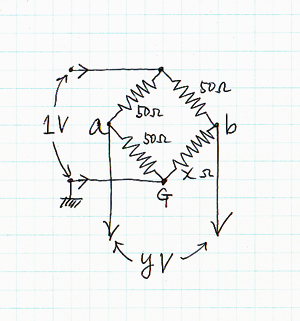
各辺が50Ω、ただし1カ所だけ未知の抵抗で構成されたブリッジがある。 x=50Ωであれば、a点b点の電位はG点を基準にして、共に0.5Vだから、y は0Vになる。 もしx=50Ωでなければ、y は0でないある値になる。その電圧を測定すれば、xΩを逆算することが出来る。 また、y=0になるように x を変化させれば、x の値を50Ωに追い込むことが出来る。 |
| 入力電圧と出力電圧の比率を求めたいので、簡単のために、最初から入力は1Vにしておく。 G点をグランドとして、a点およびb点の電位は、1Vを2個の抵抗で比例配分したものだから、右のようになる。 |
 |
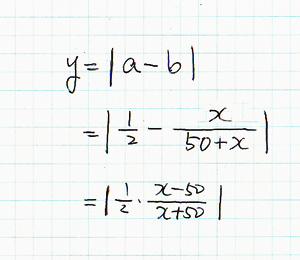 |
そうすると、出力電圧yは、左のようになる。 ただし、x が50Ωより大きいか小さいかによって符号が逆になるので、あとで対数を取る都合上、絶対値をとる。 |
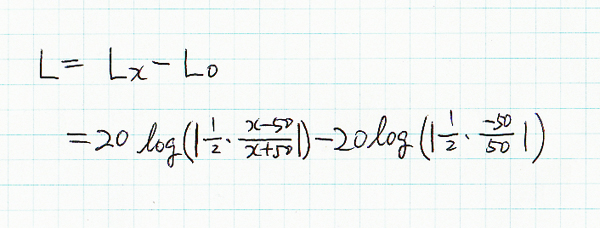 |
|
| 対数を取って、20をかけるとdBで表すことが出来る。 ただし、x の値を0Ωまたは∞Ω(つまりオープン)にした時を基準にするので、その値L0を差し引く。 そうすると上の式が、x の値からリターンロスを求める式になる。 この式を x について解けば、リターンロスから未知の抵抗 x を求めることも出来る。 さて、色々な値のダミーロードを作ったので、実測して、計算値と比較してみたのが、下の表とグラフだ。 リターンロスブリッジの性能が一番良い350MHzで測定した。 ダミーロードの抵抗値が半端なのは、偏った値のチップ抵抗で作ったからだ。たくさん買った抵抗のほとんどが96.6Ω前後だった。 ただし、50Ωはウソで、本当は48.3Ωだ。基準にするために、わざとウソをかいた。 |
|
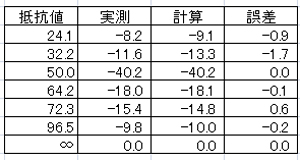 |
「実測」はダミーロードを取り替えながら、リターンロスブリッジで実測したもの。 「計算」は実際の抵抗値を上の式に入れて求めたリターンロスの値。 誤差は、その2つの差。 |
 |
|
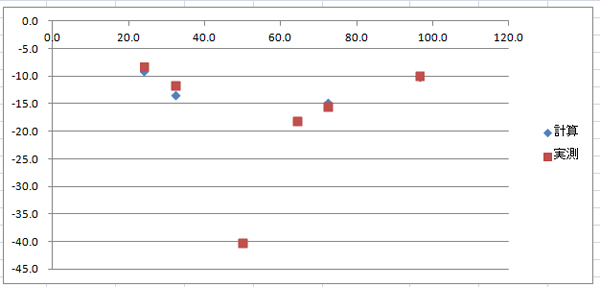
| 表では分かりにくいので、グラフにしてみた。横軸が未知の抵抗 x の値。縦軸はリターンロス。 ほとんど重なっている。 計算値は0Ωまたは∞で約6dBつまりおよそ半分くらいのロスに収束するはずだ。 また、50Ωでは出力電圧は0Vだから、ロスは無限大でなければならない。 実際には諸般の事情で無限大にはならないが、出来るだけ大きい方が「良いリターンロスブリッジ」ということになる。 |
|
 |
|
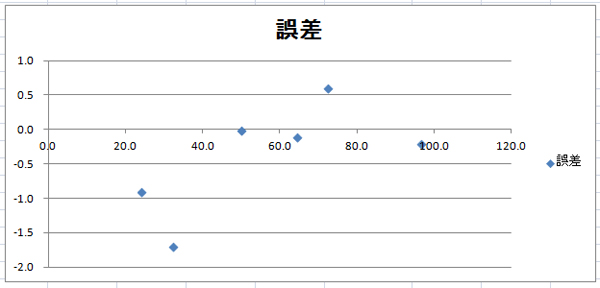
| 誤差をグラフにするとこうなる。 測定点が少ないので分かりにくいが、0Ωまたは∞で0に収束し、50Ωの近くでは誤差が大きくなるはずだ。 それにしても、最大でも誤差が2dB以内に収まっているので、SWRを測定する程度なら十分だろう。 手作りのリターンロスブリッジでも、測定器として十分間に合うということが分かった。 |
|
| |
|