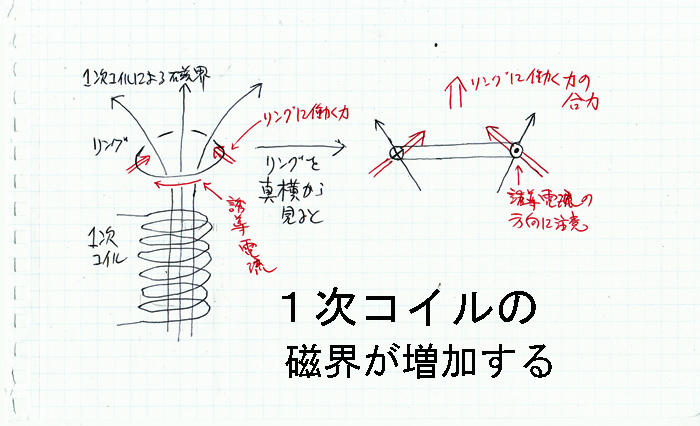
 |
【図1】ソレノイド(1次コイル)と同軸に金属リング(2次コイル)を置く。 1次コイルに電流を流して、磁界を増加させると、誘導電流が生じる。 磁界から誘導電流が受ける力の合力は、1次コイルから反発する方向に働く。 これだけならリングはコイルからはね飛ばされるはずだが。 |
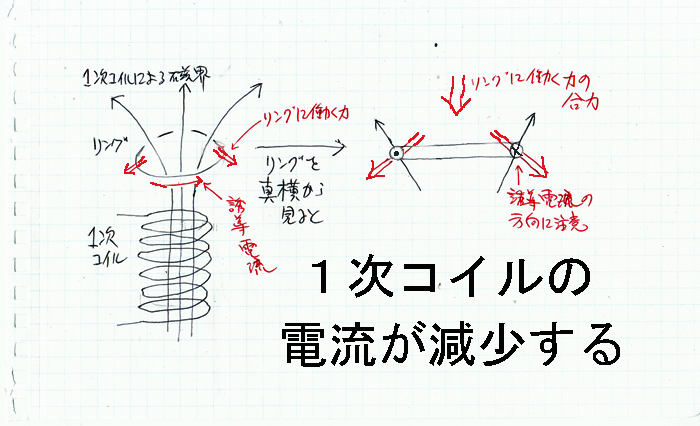 |
【図2】同じ配置で、電流が減少すると、それに応じて磁界も減少する。 誘導電流の向きは上の場合と逆になるから、磁界からリングの受ける力も逆になる。 従ってこの時、リングはコイルに引き寄せられることになる。 |
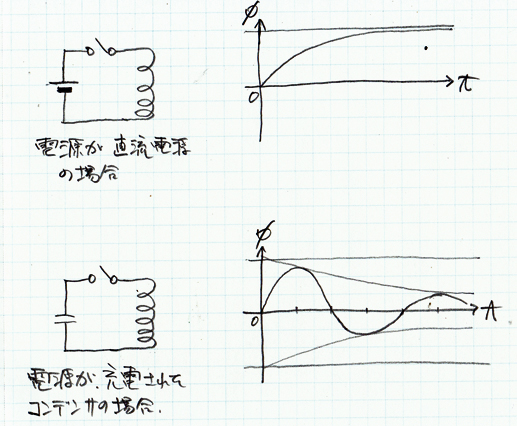 |
ディスクランチャーでは直流電源ではパワーが足りないので、強力なコンデンサを使う。 【図3】コイルに電源をつないだ場合に流れる電流の時間変化。 従って、磁界の強さも同様に変化する。 コンデンサの場合、回路が純粋にコイルとコンデンサだけなら永遠にサイン波が続くが、実際には必ず抵抗分があるので、指数的なエンベロープに従って急速に減衰する。 |
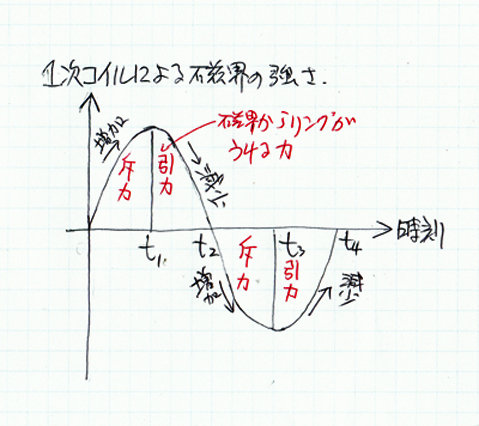 |
【図4】1次コイルに流れる電流の大きさ(従って、磁界の強さ)がどうなるかを考える。 図3で示したとおり、もし、つないだ電源が直流電源であれば、電流(従って、磁界)はある値に向かって増加し、十分な時間の後にその値に落ち着く。 しかし、電源がコンデンサであれば、電流(従って、磁界)は左図のように振動することになる。 もし、その波形が図のようにきれいなサイン波であれば、斥力と引力が1周期の間に相殺するので、リングは動かないことになる。 |
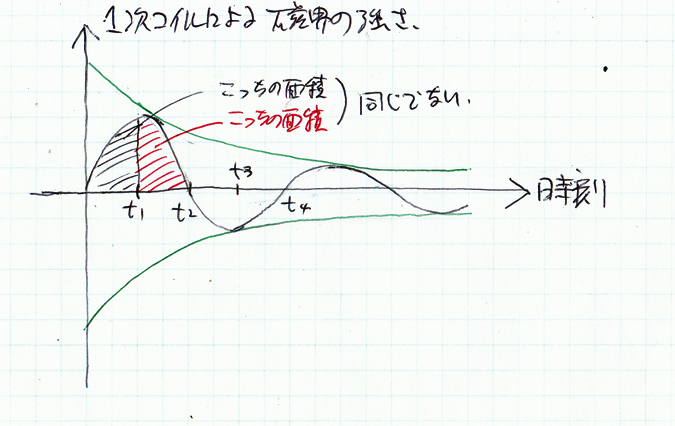 |
【図5】しかし、実際の電流(従って、磁界)の変化は左図のようになる。 従って、1次コイルの磁界によってリングが受ける力を時刻0からt2まで積分すると、わずかに正の値が残る。 t2からt4まで、さらにt4以下についても同様である。 これがディスクランチャーの原理だ。即ち、コンデンサに蓄えられたエネルギーのほとんどは相殺してしまい、わずかに波形の非対称によって残ったエネルギーが運動エネルギーに変換される。 つまりディスクランチャーは原理的に極めて能率の悪い装置だ。 |
| 試しに、5000μFのコンデンサに40Vの電圧で充電した場合を計算してみる。 コンデンサに蓄えられたエネルギーは、W=CV^2/2なので、 W=5000×10^(-6)×40^2/2=4.0(J) 位置エネルギーは、P=mghなので、このエネルギーで1円玉(0.001kg)を飛び上がらせると、 P=4.0=0.001×9.8×h → h=408(m) 400mは飛ぶはずなのに、実際には数mm程しか飛ばない。話にならないくらい能率が悪い。 |
 |
| |
↑この写真は何の関係もありません |